Genetic Algorithm for Traveling Salesperson Problem

This project was a part of a course I took in Algorithms for Data Science. Keep in mind that I was a total novice in the world of Genetic Algorithms at the time, and I may actually use this assignment as a great example of what NOT to do when writing assignments in Data Science.

Look to my blog for a post on why I think this assignment was poorly written, but I must admit that it did a great job of inspiring me to really understand Genetic Algorithms. So, here, I will present my understanding of the problem, my approach in solving it, and a Python implementation.

Problem Statement - Traveling Salesperson

A salesperson needs to visit n cities and then return to their starting city. Find the shortest path that they might take. Assume that each city can be reached along a straight line from any other city (variations of this problem may include some cities that cannot be accessed from other cities, etc.).

Genetic Algorithm Approach

Define each city as a set of xy coordinates. The “population” consists of every permutation of routes between these cities. For example, if the cities are (10, 20), (25, 40), and (50, 55), the population is:

(10, 20) (25, 40) (50, 55)

(25, 40) (10, 20), (50, 55)

(25, 40) (50, 55), (10, 20)

(50, 55) (25, 40) (10, 20)

(50, 55) (10, 20) (25, 40)

(10, 20) (50, 55) (25, 40)

Important note: This approach implies that the salesperson can start in any of the cities. This may deviate slightly from the original problem statement, depending on how you read it. But, the differences are trivial, and an implementation that fixes the starting city is a fairly simple spinoff of this approach.

Important note #2: It’s useless to actually make a list of all permutations. Instead, in Step #5 below, we simply do k random shuffles of the cities, making sure that there are no repeated routes.
Define a distance function d(r) as the sum of Euclidean distances between each successive city on route r, including from the last city back to the first.
Randomly sample k routes from the population. For each route, compute a fitness score f(r) = 1/(d(r)+1). Addition by 1 in the denominator prevents the highly unlikely scenario that a route has distance 0.
Normalize the fitness scores using the function N(f(r)) = f(r)/sum(f(r)). The sum of the Normalized scores is 1 by definition, making the fitness scores into a workable probability model.
Use the probability model to randomly select k routes with replacement. The routes with higher fitness scores are more likely to be selected. We now have k original routes and k “more fit” routes that are paired as “parents”.
Use a crossover model to breed the next generation of routes from each parent pair. a. Choose a percentage p of cities to select from parent #1. If p = 0.5, half of each child route will be from parent #1 (the theoretically “less fit” parent), so this hyperparameter can be tuned to bias more heavily towards the “more fit” parent. b. Add the selected cities from parent #1 into the child route. c. Work element-wise through parent #2, adding cities to the child route if they are not already in the child. (Hopefully, you see that this approach can be modified. There could be random selection or some other ingenious algorithm that makes better decisions about the “right” cities to choose from the fitter parent.)
Give each child route an opportunity to be “mutated.” With some small mutation rate m, if a random number x < m is selected, choose two adjacent cities on a route and swap their order.
Iterate to the next generation, using the children routes as the new sample.

Python Implementation

Import Modules

import random
import numpy as np
import itertools
import matplotlib.pyplot as plt

1. Define each city as a set of xy coordinates.

#setup cities
numCities = 8
cities = [(0,0) for i in range(numCities)]

#create random coordinates for cities on 250 x 250 grid
xmax = 250
ymax = 250

i = 0
while i < numCities:
  cities[i] = (random.randint(0,xmax), random.randint(0,ymax))
  i+=1

print(f'City Coordinates: {cities}')
plt.scatter(*zip(*cities))
plt.show()

2. Define a distance function d(r)

def calcDist(a):
  '''
  Uses Euclidean distance to find total distances of a cycle.  
  '''
  sum = 0
  for i in range(len(a)):
    #improve this by using modular arithmetic?
    if a[i] != a[-1]:
      dist = ((a[i][0] - a[i+1][0])**2 + (a[i][1] - a[i+1][1])**2)**0.5
      sum = sum + dist
    else:
      dist = ((a[i][0] - a[0][0])**2 + (a[i][1] - a[0][1])**2)**0.5
      sum = sum + dist
  return sum

3. Randomly sample k routes from the population. For each route, compute a fitness score f(r) = 1/(d(r)+1).

#sample from the population of all orders
sampSize = 5
sample = []

while len(sample) < sampSize:
  new_shuffle = random.sample(cities, numCities)
  if new_shuffle not in sample:
    sample.append(new_shuffle)

def calcFitness(sample):
  fitness_scores = []
  for route in sample:
    fitness_scores.append(1/(calcDist(route)+1)) #adding 1 in case the cycle distance is 0 somehow.

4. Normalize the fitness scores using the function N(f(r)) = f(r)/sum(f(r)).

  #normalize fitness scores to be probabilities from 0 to 1
  fitness_sum = sum(fitness_scores)
  for index, score in enumerate(fitness_scores):
    fitness_scores[index] = score / fitness_sum
  return fitness_scores

5. Use the probability model to randomly select k routes with replacement.

def newSample(fitness_scores, sample):
  new_sample = []
  #make decision boundaries
  boundaries = [0]
  for index, score in enumerate(fitness_scores):
    boundaries.append(boundaries[index] + fitness_scores[index])

  for i in range(len(sample)):
    rand_num = random.random()
    k = -1
    for boundary in boundaries:
      if rand_num < boundary:
        new_sample.append(sample[k])
        break
      else:
        k+=1      
  return new_sample

6. Use a crossover model to breed the next generation of routes from each parent pair.

def crossover(numCities, sampSize, sample, new_sample):
  '''
  Returns the array of children composed of approximately 50/50 slices
  of each parent (sample and new_sample).
  '''
  children = []
  num_from_parent1 = numCities//2
  for i in range(sampSize):
    #contribution of parent #1
    start = random.randint(0, num_from_parent1)
    child = [(0,0) for i in range(numCities)]
    child[0:num_from_parent1] = sample[i][start:start+num_from_parent1]
    #contribution of parent #2
    for index, city in enumerate(child):
      if city == (0, 0):
        for city2 in new_sample[i]:
          if city2 not in child:
            child[index] = city2

    children.append(child)

  return children

7. Give each child route an opportunity to be “mutated.”

def mutate(children, rate, numCities):
  '''
  returns the children array with adjacent pairs swapped if the mutation rate is
  triggered.  Allows user to set a mutation rate.
  '''
  mutation_trigger = random.random()
  for order in children:
    if mutation_trigger < rate:
      indexA = random.randint(0, numCities-1)
      indexB = (indexA + 1) % numCities
      temp = order[indexA]
      order[indexA] = order[indexB]
      order[indexB] = temp
  return children

Overall Function Structure

Set Up, Hyperparameters, Initialization

#setup cities
numCities = 8
cities = [(0,0) for i in range(numCities)]

#create random coordinates for cities on 250 x 250 grid
xmax = 250
ymax = 250

i = 0
while i < numCities:
  cities[i] = (random.randint(0,xmax), random.randint(0,ymax))
  i+=1

print(f'City Coordinates: {cities}')
plt.scatter(*zip(*cities))
plt.show()

#sample from the population of all orders
sampSize = 5
sample = []

while len(sample) < sampSize:
  new_shuffle = random.sample(cities, numCities)
  if new_shuffle not in sample:
    sample.append(new_shuffle)
    
for s in sample:
  print(s) #verify

#define best route distance to be infinity
current_best_dist = np.inf

#define best route as None
current_best_route = None

#set mutation rate
rate = 0.01

Unifying Function Structure

def GA(sample, current_best_dist, current_best_route, numCities, sampSize, rate):

  #Step 1:  Calculate Distances and Find Best Route
  current_best_dist, current_best_route = bestRoute(sample, current_best_dist, current_best_route)

  #Step 2:  Give Fitness Scores and Normalize to Probabilities
  fitness_scores = calcFitness(sample)

  #Step 3:  Use Probability Weights to Select New Sample
  new_sample = newSample(fitness_scores, sample)

  #Step 4:  Implement Crossover Function with Parent #1 from original sample and Parent #2 from new sample
  children = crossover(numCities, sampSize, sample, new_sample)

  #Step 5: Mutate
  sample = mutate(children, rate, numCities)
  #Repeat on Mutated Children (ha! like x-men!)

  return sample, current_best_dist, current_best_route

Tracking Best Routes

This helper function graphed the current best route as soon as it was found.

def bestRoute(sample, current_best_dist, current_best_route):
  for route in sample:
    current_distance = calcDist(route)
    if current_distance < current_best_dist:
      current_best_dist = current_distance
      current_best_route = route
      print(f'BETTER ROUTE FOUND!')
      print(f'Current Best Route: {current_best_route}\nDistance: {current_best_dist}\n')
      figure, axis = plt.subplots()
      plt.plot(*zip(*current_best_route), '-o')
      plt.show()
  return current_best_dist, current_best_route

For the entire implementation, check out the Colab notebook here.

Results

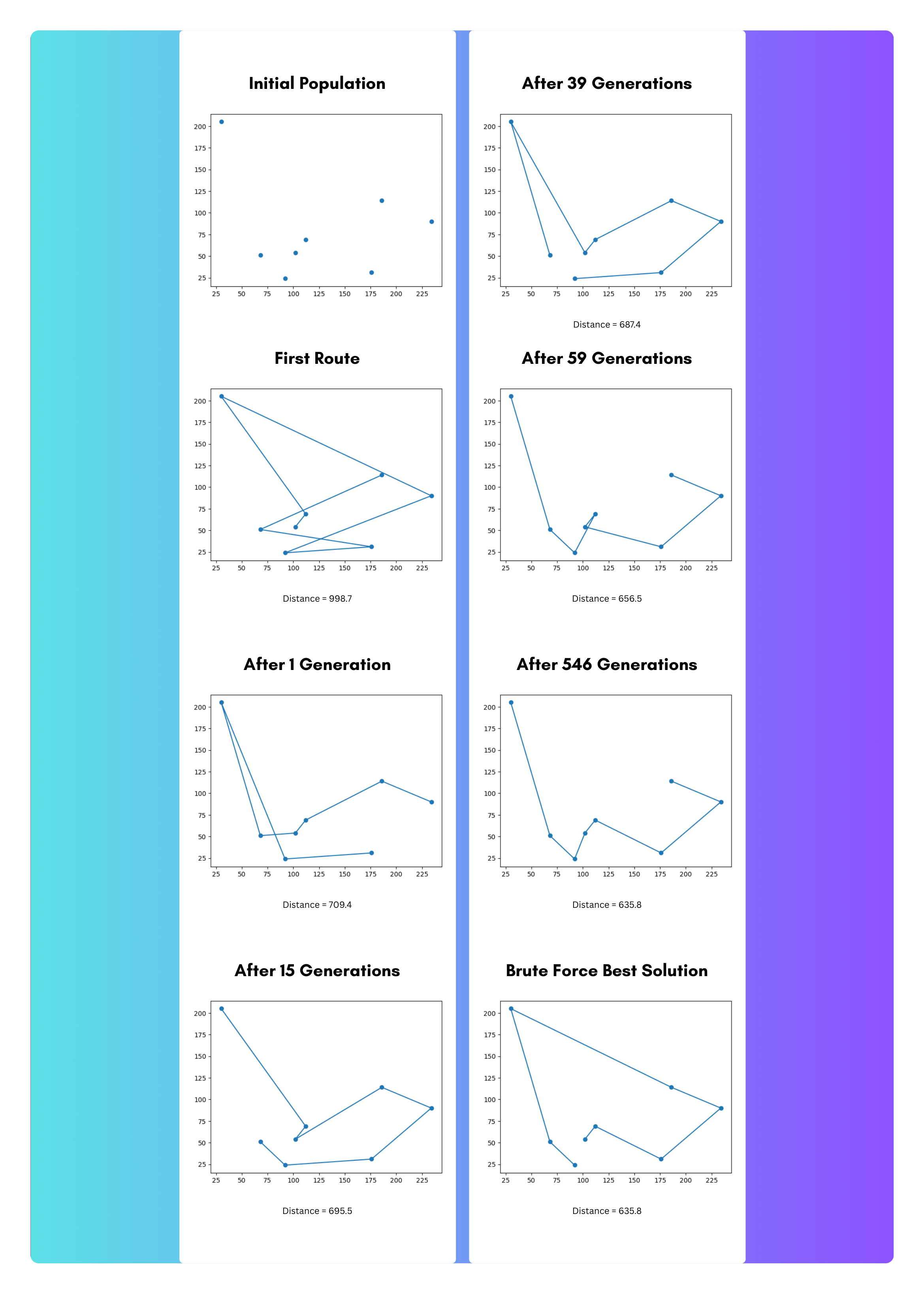
First, let’s walk through a single run of the notebook. I arbitrarily decided to run this for 8 randomly selected city locations.

To assess the performance of the algorithm, I also ran the brute force method, where all routes were searched and the best distance was recorded. This isn’t a practical algorithm for this problem, as the time complexity increases factorially. But, for just 8 cities, the brute force algorithm didn’t take too long to find the optimal path with a distance of 635.8.

The genetic algorithm took 546 generations to find this optimal path, which completed in less than 30 seconds.

If we aren’t satisfied with 500+ generations to find a good solution, it should be noted that a solution with distance 648.4 was found on Iteration 92, which is about 2% off from optimal. So, we can be reasonably confident that this algorithm efficiently finds near optimal solutions, and will eventually find optimal solutions.