Genetic Algorithm – Knapsack Problem
A Genetic Algorithm for Solving the 0-1 Knapsack Problem
A classic problem in computer science, the 0-1 Knapsack is a great way to test out different implementations of a genetic algorithm, then comapre them with a simpler greedy algorithm, which tends to solve this problem quite well.
Problem Statement
Given a set of items with known weights and values, we want to pack a knapsack that maximizes the value of the items inside without exceeding the knapsack’s maximum capacity.
Algorithm Overview
Problems like this can be tricky to find optimal solutions. As the number of items in the population increases, the time complexity of the problem increases exponentially.
Genetic algorithms allow us to start with potential solutions at random, then iteratively select the best (or “fittest”) solutions across many generations. As the name implies, this behaves very much like evolution. The chief ingredients are:
- A metric for assessing the “fitness” of a particular solution.
- A method for creating the next generation that is biased towards fitter solutions.
- An occasional injection of randomness (or mutation) so that we don’t converge on a less-than-optimal solution too soon.
My algorithm for this problem included the following steps:
- Initialize the algorithm with randomly selected groups of items (i.e. potential knapsack solutions) from the population (more later about how to do this sensibly)
- Score each knapsack solution. If the weight of the items is within capacity, its score is simply the value of the items inside. If the items are overweight, we successively remove items based on their value-to-weight ratio until the items are within capacity.
- Use the scores to create a probability model. We want the fittest solutions to be more likely to breed into the next generation.
- Use the probability model to randomly select (with replacement) from the current group of knapsacks. The fittest ones are more likely to be selected.
- We now have a set of original knapsacks and a set of “fitter” knapsacks. These sets are the same size. We pair them together for breeding.
- Use a crossover model to combine items from each parent pair: a. We first randomly select b% of the items from the original knapsack, where b is a tuned hyperparameter. A smaller b selects less from the original knapsack and more from the “fitter” knapsack mate. b. Then, we randomly select items from the “fitter” parent until the knapsack fills up or exceeds the weight limit. c. If the weight limit is exceeded, greedily remove the worst value-to-weight items from the knapsack until the weight constraint is satisfied. d. Repeat for each parent pair.
- Use a mutation model for the new set of “children” knapsacks: a. Set a mutation rate r between 0 and 1 and generate a random real number x between 0 and 1. b. If $x < r^3$, we swap out 10 items randomly with items from the population. c. Otherwise, if $x < r^2$, we swap out 3 items. d. Otherwise, if $x < r$, we swap out 1 item. e. Otherwise, no swaps occur.
- Search through the children knapsacks for the current best solutions. Be sure to keep them.
- Repeat for many generations, using the new children as the next set of knapsacks to be scored in step 2.
Algorithm Implementation
Imports
import random
import matplotlib.pyplot as plt
from tqdm import tqdm
import numpy as np
Functions
1. Initialize the algorithm with randomly selected groups of items
def inclusionRates(pop, max_capacity, sample_size):
'''
Generates a distribution of inclusion rates based on binomial probabilities,
where p is the probability that an item will be selected for the knapsack,
and p is the E(Items that will fit) / N, the population size (which is itself
Capacity/Total Weight)
Then, the distribution is binomial with mean population size * p and variance
population size * p * (1-p)
We want to bias against knapsacks that are overweight, so we will generate
inclusion rates that will select from about 2 standard deviations below the
expected number of items up to one half of a standard deviation above
the expected number of items
'''
pop_weight_total = sum([b[0] for b in pop])
p = max_capacity/pop_weight_total
rates = []
while len(rates) < sample_size:
rate = np.random.normal(loc = 0.9 * p, scale = 0.05 * p)
rates.append(min(max(rate, 0), p))
return rates
def getInitialChromosomes(sample_size, pop_size, inclusion_rates):
'''
Uses distributed inclusion rates to make lists of chromosomes,
sets of 0's and 1's equal to the population size, where 0 indicates an
item that should not be packed into the knapsack, and 1 indidicates an
item that should be packed.
'''
chromosomes = []
for inclusion_rate in inclusion_rates:
included_items = [random.randint(1,100) for _ in range(pop_size)]
threshold = int(100*inclusion_rate)
for index, item in enumerate(included_items):
if item <= threshold:
included_items[index] = 1
else:
included_items[index] = 0
chromosomes.append(included_items)
return chromosomes
def pack(pop, chromosomes_list):
'''
Uses the chromosome lists to "pack" a knapsack - taking the indexed
items from the population
'''
knapsacks = []
for chromosomes in chromosomes_list:
knapsack = [pop[index] for index, chromosome in enumerate(chromosomes) if chromosome == 1]
knapsacks.append(knapsack)
return knapsacks
2. Score each knapsack solution.
def weight(knapsack):
'''
compute the total weight of a collection of items in knapsack
'''
return sum([item[0] for item in knapsack])
def value(knapsack):
'''
compute the total value of a collection of items in knapsack
'''
return sum([item[1] for item in knapsack])
def fitness_score(knapsack, max_capacity):
'''
Gives fitness score to each knapsack and repairs overweight knapsacks greedily
'''
return value(repair_overweight(knapsack, max_capacity))
def repair_overweight(knapsack, max_capacity):
'''
Removes lowest value-to-weight items from overweight knapsacks
'''
if weight(knapsack) <= max_capacity:
return knapsack
sorted_knapsack = sorted(knapsack, key = lambda x: x[1]/x[0])
while weight(sorted_knapsack) > max_capacity:
sorted_knapsack.pop(0)
return sorted_knapsack
3. Use the scores to create a probability model.
def decision_boundaries(all_fitness_scores):
'''
Accumulates fitness scores additively into list, creating boundaries for parent
selection
'''
boundaries = [0]
for index, (knapsack, fitness_score) in enumerate(all_fitness_scores):
boundaries.append(boundaries[index] + fitness_score)
return boundaries
4. Use the probability model to randomly select (with replacement) from the current group of knapsacks.
def generateFitterParents(boundaries, knapsacks):
'''
We need a group of parents that are as fit as possible while preserving
some random chance, diversity, etc. in the algorithm. So, this uses
the decision boundaries made before to probabilistically choose a sample
of knapsacks. More fit (i.e. higher value) knapsacks are more likely (but not guaranteed)
to be chosen. Knapsacks with fitness scores of 0 cannot be chosen.
'''
fitter_knapsacks = []
while len(fitter_knapsacks) < len(knapsacks):
random_number = random.uniform(0, max(boundaries))
for index, boundary in enumerate(boundaries[1:]):
if random_number < boundary:
fitter_knapsacks.append(knapsacks[index])
break
return fitter_knapsacks
5. Pair original knapsacks and fitter knapsacks together for breeding.
parents = zip(knapsacks, fitter_knapsacks)
6. Use a crossover model to combine items from each parent pair.
def crossover(knapsack, fitter_knapsack, max_capacity, bias):
'''
This algorithm will take each knapsack and pair it with its corresponding
"fitter" knapsack.
First, we randomly select a percentage of the items in the original knapsack.
These are the first items placed into the child knapsack.
This includes a bias hyperparameter that can be tuned - the percentage
of the original knapsack to take. Including 50% or more of the original
may preserve more diversity, but including less than 50% of the original
may push evolution more quickly towards convergence.
Then, we work element-wise through the fitter knapsack, adding elements to the child
only if they are not already in the child.
There are cases where the child knapsack could be overweight. In this case,
we recursively call the crossover function to retry the algorithm with a harsher
bias towards the first parent.
'''
num_to_sample = int(len(knapsack) * bias)
selected_indices = random.sample(range(len(knapsack)), k = num_to_sample)
child = []
for index in selected_indices:
child.append(knapsack[index])
child_weight = weight(child)
shuffled_fitter_knapsack = fitter_knapsack[:]
random.shuffle(shuffled_fitter_knapsack)
for item in shuffled_fitter_knapsack:
if item not in child and item[0] + child_weight <= max_capacity:
child.append(item)
child_weight += item[0]
if weight(child) > max_capacity:
bias = bias/2
return crossover(knapsack, fitter_knapsack, max_capacity, bias)
else:
return child
Use a mutation model for the new set of “children” knapsacks.
def swapOne(child, pop):
'''
Helper function to be used with mutate. Swaps a random item from the population
into a child knapsack.
'''
if len(child) == 0:
return child #no swap
while True:
swap_in = random.choice(pop)
if swap_in not in child:
break
index_to_replace = random.randint(0, len(child)-1)
child[index_to_replace] = swap_in
return child
def mutate(children, pop, rate):
'''
To preserve diversity in each generation, we want to occasionally mutate.
This function will replace 0, 1, 2, or 3 items in the knapsack with a
random item from the population that isn't already in the knapsack.
To pick the number of items to be replaced, we use a geometric probability
model:
P(1 item is replaced) = rate
P(3 items are replaced) = rate squared
P(10 items are replaced) = rate cubed
'''
mutated_children = []
for child in children:
trigger = random.random()
if trigger < rate**3:
for _ in range(10):
child = swapOne(child, pop)
elif trigger < rate**2:
for _ in range(3):
child = swapOne(child, pop)
elif trigger < rate:
child = swapOne(child, pop)
mutated_children.append(child)
return mutated_children
8. Search through the children knapsacks for the current best solutions.
def preserve_elites(all_fitness_scores, mutated_children, num_of_elites):
'''
For each generation, we make sure that the two (or more) best knapsacks are
preserved.
'''
elites = sorted(all_fitness_scores, key = lambda x: x[1], reverse = True)[:num_of_elites]
elite_knapsacks = [e[0] for e in elites]
mutated_children = sorted(mutated_children, key = lambda x: x[1], reverse = False)
return elite_knapsacks + mutated_children[num_of_elites:]
Unifying Function Structure/Calls
def initializeKnapsackGA(pop, pop_size, max_capacity, sample_size):
'''
Step 1: Collect the sample of chromosomes
'''
inclusion_rates = inclusionRates(pop, max_capacity, sample_size)
chromosomes_list = getInitialChromosomes(sample_size, pop_size, inclusion_rates)
'''
Step 2: Use selected chromosomes to select sample of knapsacks
'''
knapsacks = pack(pop, chromosomes_list)
return knapsacks
def knapsackGA(knapsacks, pop, iter_num, max_capacity, num_iterations, bias, sample_size):
'''
Step 3: Generate fitness score for each knapsack in sample
'''
all_fitness_scores = [(knapsack, fitness_score(knapsack, max_capacity)) for knapsack in knapsacks]
'''
Step 4: Make list of decision boundaries
'''
boundaries = decision_boundaries(all_fitness_scores)
'''
Step 5: Use decision boundaries to generate sample of most fit knapsacks
'''
fitter_knapsacks = generateFitterParents(boundaries, knapsacks)
'''
Step 6: Breed original knapsacks with fitter knapsacks
'''
parents = zip(knapsacks, fitter_knapsacks)
children = []
for knapsack, fitter_knapsack in parents:
children.append(crossover(knapsack, fitter_knapsack, max_capacity, bias = bias))
'''
Step 7: Mutate
'''
mutated_children = mutate(children, pop, rate = 0.2)
'''
Step 8: Preserve Elites
'''
mutated_children = preserve_elites(all_fitness_scores, mutated_children, num_of_elites = int(sample_size*0.1))
'''
Step 9: Compute average and maximum fitness score for mutated children
'''
new_fitness_scores = [fitness_score(child, max_capacity) for child in mutated_children]
avg_fitness_score = sum(new_fitness_scores)/len(new_fitness_scores)
max_fitness_score = max(new_fitness_scores)
'''
Step 10: Return mutated children for next generation
'''
return mutated_children, avg_fitness_score, max_fitness_score
Main Code
pop_size = 500
pop = [(random.randint(5,50), random.randint(10,100)) for i in range(pop_size)]
pop_value_total = sum([a[1] for a in pop])
pop_weight_total = sum([b[0] for b in pop])
sample_size = 50
num_iterations = 10000
#define max capacity of knapsack to be half the total weight of all items
max_capacity = pop_weight_total/2
#get first sample of knapsacks
gen = initializeKnapsackGA(pop, pop_size, max_capacity, sample_size)
average_fitness_scores = []
max_fitness_scores = []
bias = 0.3
#iterate through generations of knapsacks
for i in tqdm(range(num_iterations)):
gen, avg_score, max_score = knapsackGA(gen, pop, num_iterations = num_iterations, iter_num = i, max_capacity=max_capacity, bias = bias, sample_size = sample_size)
bias = bias/1.02 #over generations, reduce influence of parent #1 in favor of fitter parent #2
average_fitness_scores.append(avg_score)
max_fitness_scores.append(max_score)
print(f"Max Capacity of Knapsack: {max_capacity}")
print(f"Last Generation Weight: {weight(gen[0])}")
print(f"Last Generation Max Value: {max_fitness_scores[-1]}")
print(f"Best Value: {max(max_fitness_scores)}")
Visualize
We want to see that the fitness scores (i.e. value of items in appropriately-weighted knapsacks) are increasing towards some optimal value. We also want to verify that there is enough mutation, diversity, and randomness that the algorithm won’t get stuck. Therefore, I visualized both the best value knapsack and the average value knapsack in each generation.
def fitnessScoreGrapher(average_fitness_scores, max_fitness_scores):
'''
Graphs fitness score for each generation of knapsacks.
In black, graph average fitness score of the generation.
In red, graph maximum fitness score of the generation.
'''
xvals = list(range(0, len(average_fitness_scores)))
yvals = average_fitness_scores
y2vals = max_fitness_scores
plt.plot(xvals, yvals, linestyle = '-', marker = 'o', color = 'black', label = "Average Value")
plt.plot(xvals, y2vals, linestyle = '--', marker = 'x', color = 'red', label = "Max Value")
plt.xlabel("Iteration")
plt.ylabel("Fitness Score (Value)")
plt.title("Convergence Plot for Knapsack Value")
plt.grid(True)
plt.legend()
plt.xlim(0, max(xvals)+1)
plt.ylim(min(yvals)-100, max(y2vals)+100)
plt.show()
Results
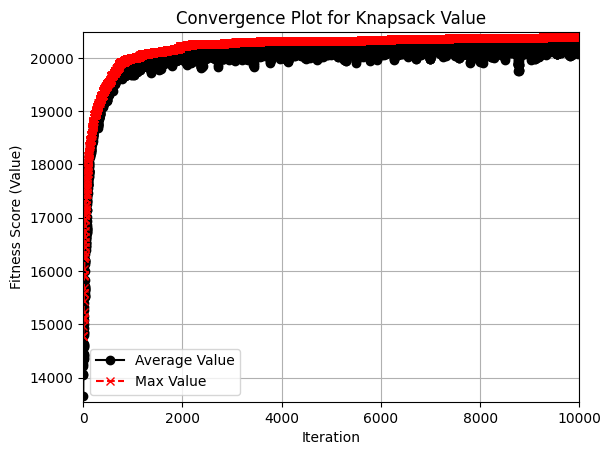
The convergence plot shows a couple of nice behaviors of this algorithm.
First, the algorithm continually improves throughout the generations. This is largely thanks to the greedy removal of items from overweight knapsacks and the preservation of “elite” (i.e. best-value) knapsacks from one generation to the next.
Second, the average values (shown in black) show a fair amount of noise as the generations progress. This indicates that enough randomness is preserved by the algorithm so that it doesn’t converge prematurely.
The question is - How do we know that we are converging towards an optimal/near-optimal solution, and not some much worse solution? We can compare the performance of this algorithm to a deterministic one. For example, greedy algorithms tend to do quite well with the 0-1 Knapsack problems because of the simplistic metrics that can be used to sort the population (in this case, value/weight ratio). The genetic algorithm implementation above performed about 5% worse than the greedy algorithm. So, the genetic algorithm (which would outperform greedy in time and space complexity) performs adequately.